Multi-Agent Actor-Critic RL

Atari game을 통해 강화학습의 가능성을 보여준지도 꽤 시간이 지났다. 그 이후 강화학습은 AlphaGo를 통해 다시한번 세상의 이슈가 되었으며, 이 블로그에도 관련 기술을 소개한 바 있다. 이후 DeepMind사는 Starcraft를 상대할 것이라는 이야기가 회자되었다. 하지만 Starcraft game의 정복은 쉽지 않을 것이란 예상이 많았다. 근본적인 이유는 게임 자체가 정해진 틀이 없는 전략 게임이라는 점도 있지만, 다수의 agent들간의 상호 협력 또는 적대적 플레이를 해야 한다는 점이다. Agent들은 독립적으로 움직이면서 상호 협력하거나 적대적 대응을 해야 하며, MDP관점에서 battle ground 뿐만 아니라 agent 자신을 제외한 모든 agent들도 environment가 된다는 점과, 이 agent들이 지속적을 자체 학습을 통해 진화하는 상황에서의 학습이라는 점도 쉽지 않을 것이라는 이유이다. DQN과 같은 알고리즘을 사용한다고 할때 알고리즘의 안정화에 필수적인 replay buffer의 사용과 이 buffer의 sample은 계속 진화하고 있는 환경에도 적합한 방법인지 알 수 없다. 또한 multi-agent environment에서 policy network가 학습이 가능할지도 의문이다.

이번에 분석한 논문은 이러한 수 많은 의문에 하나의 가능성을 보여준 논문으로, 다수의 agent들이 참여하여 특정 목적을 달성하도록 학습시키는 강화학습에 관한 내용이다. 하나의 agent의 학습을 위한 여러 이론도 중요하지만 다수의 agent들을 동시에 학습시킨다는 개념은 실제적인 응용면에서 매우 중요한 의미를 가진다는 것을 알기에 이 논문을 읽어보았다. 논문은 아래 제목으로 발표되었고, 일명 Multi-Agent Deep Deterministic Policy Gradient(MADDPG)라고 부른다. DDPG를 multi-agent환경에 적용한 논문이므로 앞서 올린 글과도 직접적으로 관계가 있다.

Multi-Agent Actor-Critic for Mixed Cooperative-Competitive Environments

이 논문에서는 actor-critic policy gradient를 기본으로 한다. 일단, actor는 다른 agent의 policy를 안다는 가정(미리 안다는 가정)을 사용해서는 안된다. Agent는 관측가능한 기본적 observation 정보만 이용하여 판단하고 행동해야 한다. 반면 critic관점에서 보면 action-value function은 자기 자신의 policy에 기반하여 계산되지만, 다른 agent들의 action에 어떤 형태든 대응하지 않고 나홀로 독립적으로 행동한다면 이 논문의 목적하고는 거리가 먼것이라고 할 수 있다. 학습하는 agent들은 다른 agent들의 policy변화에 능동적으로 반응하여 최적의 action을 찾아 내야 한다. 이 논문은 살펴보면 볼수록 DDPG의 단순한 확장은 아니라는 생각이 들었고, 이해 하기도 쉽지 않다.

Multi-agent MDP와 DDPG

우리가 함수를 다룰때 변수의 범위나 space/dimension을 중시하는 것처럼, MDP에서도 State, Action, Policy등의 특징과 space를 반드시 확인할 필요가 있다. 그동안 RL은 주로 single agent의 MDP문제였으나, MADDPG는 MDP를 다른 시각으로 볼 필요가 있다. MADDPG에서는 모든 agent의 거동이 감안된 state space $\mathcal{S}$ , 각 agent들의 개별적 observation space $\mathcal{O}$ 와 action space $\mathcal{A}$ , agent별로 Observation과 Action space의 곱으로 표현하는 stochastic policy space $\mathcal{O} \times \mathcal{A}$ , 마지막으로 state space와 모든 agent들의 action space들의 곱으로 표현되는 Transition space $\mathcal{T}$ 가 있다. 각 agent들은 state와 action space의 곱과 같은 reward space를 갖게 된다.

Multi_agent Actor-Critic

MADDPG에서는 critic으로 DQN에서 사용하는 Q-value network를 사용한다. Actor는 RL의 Policy Gradient method를 사용하여 학습시킨다. 적대적(adversarial) 또는 협동적(cooperative) agent들의 개별적인 actor network를 가지되, 방향성/목표를 유도하려고 centralized critic을 사용 한다. 이 구조를 논문에서는 아래 그림을 이용하여 “centralized training with decentralized execution” 이라고 표현하고 있다. 한장의 그림이 모든걸 표현하기도 한다. 좋은 논문은 이런식으로 이론을 일목요연하게 표현하려고 하고 이론의 전체적인 틀을 보는데 이만한 것이 없다는 생각이 든다. 수학식들중 중요한 식들은 적어 놓았지만 전체 내용은 논문을 참조하기 바란다.

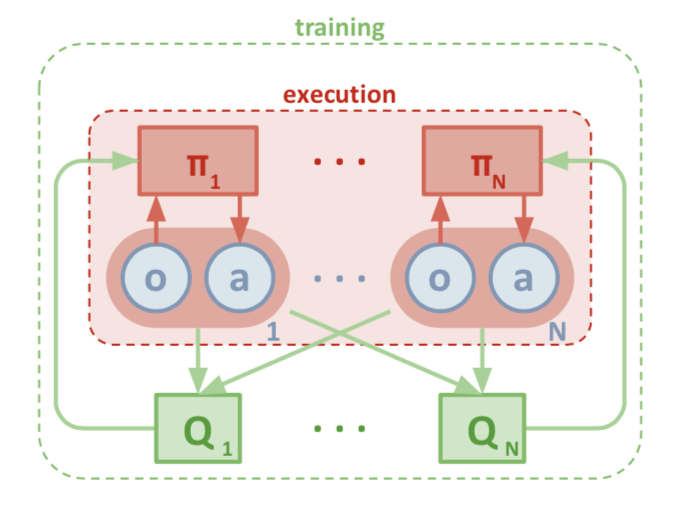
MADDPG

Policy gradient 방법은 discounted cumulative reward $J$ 의 최대화를 목표로 하며, multi-agent deterministic policy gradient는 아래와 같이 표현할 수 있다.

$\nabla_{\theta_i} J({\mu_i}) = \mathbb{E}_{\textbf{x},a{\sim}D} \left [ \nabla_{\theta_i} \mu_i (a_i|o_i) \nabla_{a_i} Q^{\mu}_i (\textbf{x},a_1,...,a_N )|_{a_i = \mu_i (o_i)} \right ]$

여기서, Q-value를 보면 state와 모든 agent의 action을 감안한 함수로 표현해 놓은 것을 알 수 있으며, 위 그림에서도 이를 잘 나타내고 있다. 즉 training 과정에서 Q-value를 구하는 과정에서 모든 agent들의 action이 고려된다는 것을 의미하므로 muti-agent가 포함된 환경에서 action-value를 구하고 training하므로 각 agent들은 다른 agent가 포함된 environment에서 policy를 최적화 할 수 있는 것이다. 그러므로, 이 action-value function을 centralized action-value function이라고 부르는데, 모든 agent의 action $a_1,...,a_N$ 와 state information $\textbf{x}=(O_1, ..., O_N)$ 을 입력으로 받아, agent $i$ 의 action-value function을 구한다. Experience replay buffer $\mathcal{D}$ 는 tuple $(\textbf{x},a_1, ..., a_N,r_1,...,r_N, \textbf{x}')$ 형태로 모든 agent들의 experience를 저장한다.

Centralized action-value function $Q^{\mu_i}$ 는 아래와 같은 식으로 update된다.

$\mathcal{L}(\theta_i) = \mathbb{E}_{\textbf{x},a,r,\textbf{x}'} \left [(Q^{\mu}_i (\textbf{x},a_1,...,a_N ) - y)^2 \right]$

$y=r_i + \gamma Q^{\mu'}_i (\textbf{x}', a'_1, ..., a'_N )|_{a'_j = \mu'_j (o_j)}$

여기서, $\mu' = \{\mu_{\theta'_1} , ..., \mu_{\theta'_N}\}$ 로 target policy의 집합을 의미한다. 그런데, 이 식을 보면 next state에서 다른 agent들의 다음 action을 알아내서 target Q-value를 구해야 update가 가능하다는 점을 알 수 있다. 즉, 어떤 방법을 통해 다른 agent들의 policy를 알아 낼 수 있다면 위의 식을 그대로 사용할 수 있다. Q-learning구조에서는 당연한 것이나, 이러한 전제조건은 일견 문제를 복잡하게 만든다는 것이 분명하다. 다른 agent들도 environment의 일부라는 관점에서 보면 마치 environment의 model(전체가 아니더라도..)을 알고 있다는 의미로 해석될 수 있다. 그러나, MADDPG는 model-free 알고리즘이므로, 다른 agent들의 policy를 traning중에 학습하게 된다면, environment의 model을 학습하는 과정(model learning)을 통해서 문제를 풀어가는 Dyna 알고리즘과 유사하다고 생각할 수도 있다. 다른 관점에서, agent들은 모두 행동의 주체이고 agent 집합체의 Q-learning이라고 생각한다면 기존의 model-free actor-critic과 다르지 않다고 생각할 수 있다. 이제서야 왜 저자가 “centralized training”이라는 용어를 사용했는지 짐작이 간다. (내 해석이 맞는다면…)

Agent policy 추론

그러므로 이제 agent 집합체가 개별적 학습과정을 통해 policy를 upgrade시키도록 고안해야 하고, 이 policy가 반영된 action에 의한 q-value가 점차 target에 가까워 져야 한다. 내 생각에 이 문제는 최대 난관이라고 생각한다. 잘못하면 학습이 불가능하거나 local optimum에서 헤어나지 못할지도 모른다. 논문에서는 다른 agent들의 policy를 추론할 수 있는 방법에 대해 설명하고 있다. Agent $i$ 는 추가로 다른 agent $j$ 의 true policy $\mu_j$ 에 대응하는 approximation policy $\hat{\mu}^j_i$ 를 지속적으로 추론하도록 한다. 다른 agent들의 approximation policy는 action의 log probability를 최대화 시키는 방향으로 추론하였으며, entropy regularizer( $H$ )를 도입하였다. 이와 같이 추론된 policy를 논문에서는 “approximate policy”라고 부른다.

$\mathcal{L}(\phi^j_i) = - \mathbb{E}_{o_j , a_j} \left [log \hat{\mu}^j_i (a_j | o_j ) + \lambda H(\hat{\mu}^j_i ) \right]$

$\phi$ 는 policy approximator의 패러미터를 의미한다. 이 추정 policy를 사용하여 위 식의 $y$ 는 approximate value $\hat{y}$ 로 대체할 수 있다.

$\hat{y}=r_i + \gamma Q^{\mu'}_i (\textbf{x}', \hat{\mu}'^1_i (o_1), ...,\hat{\mu}'^N_i (o_N) )$

위 식은 Q-learning의 target network의 함수이고 off-policy 방식의 update라고 생각할 수 있다.

Agent Policy Ensembles

이 블로그에서 DQN을 소개하면서 알고리즘의 안정성을 확보하기 위한 기술들을 언급하였으나, DQN 기술을 차용한다손 치더라도 muti-agent들이 참여하는 environment에서 알고리즘의 안정성 문제는 훨씬 어려운 문제임을 짐작할 수 있다. Agent들이 계속해서 자신의 policy를 변화시키는 non-stationary environment에서 다른 agent의 policy변화에 너무 적극적으로 자신의 policy를 update시키게 된다면 알고리즘의 안정성을 해치게 될것이다. 이 문제를 해결하기 위해 논문에서는 $K$ 개의 서로 다른 sub-policy로 이루어진 policy의 ensemble을 훈련시키는 방법을 도입하였고, 매 episode마다 각 agent가 실행시킬 sub-policy를 무작위로 선택하여 사용한다.

이제 $\mu_i$ 는 agent $i$ 가 가지는 하나의 policy가 아니라 K개의 sub-policy로 이루어진 ensemble을 나타낸다. 이 ensemble에서선택된 policy $k$ 는 $\mu^{(k)}_i$ 로 표기하고 아래식과 같이 ensemble objective를 최대화 시키도록 학습시킨다.

$J_e (\mu_i ) = \mathbb{E}_{k \sim unif(1, K), s\sim p^{\mu} , a \sim \mu^{(k)}_i } \left [ R_i (s,a) \right ]$

episode마다 다른 sub-policy가 실행되기 때문에 agent $i$ 의 각 sub-policy $\mu^{(k)}_i$ 에 대해 replay buffer $\mathcal{D}^{(k)}_i$ 를 운영하며, ensemble objective의 gradient는 아래 식으로 표현할 수 있다.

$\nabla_{\theta_i^{(k)}} J_e ({\mu_i}) = \frac {1}{K} \mathbb{E}_{\textbf{x},a \sim D^{(k)}_i} \left [ \nabla_{\theta_i^{(k)}} \mu_i^{(k)} (a_i|o_i) \nabla_{a_i} Q^{\mu}_i (\textbf{x},a_1,...,a_N )|_{a_i = \mu_i^{(k)} (o_i)} \right ]$

Policy ensemble에서는 일종의 policy basket을 운영하겠다는 얘기인데, episode마다 다른 policy를 운영하게 되면 학습을 위한 data창고인 replay buffer도 별도로 운영한다. 이것을 policy가 일종의 distribution을 가진다고 생각해 볼 수 있다. 무작위 sampling을 한다면 uniform distribution으로 볼 수 있다. 이 논문은 해석하는데 적잖은 시간이 필요하다. 그러면서도, 완전히 이해한것인지 불분명하다.

마지막으로 논문에서 밝힌 MADDPG의 pseudo-code는 아래와 같다.

MADDPG_Algorithm

이 code는 DDPG의 code와 비슷해 보이지만, 첨자들에 여기서 소개한 많은 내용이 내포되어 있다. DDPG에서는 replay buffer에서 sampling한 sample을 위한 첨자만 필요했지만, MADDPG에서 $i$ 는 agent를 위한 첨자이며, $j$ 는 replay buffer에서 sampling한 sample을 위한 첨자이고, 마지막으로 $k$ 는 policy ensemble에서 sampling한 policy를 위한 첨자이다.

테스트

Multi-agent RL 자료를 살펴보면 OpenAI의 multiagent-particle-envs를 활용하여 다양한 시나리오에서 구현한 실험을 찾아 볼수 있다. 최근 Dota2 game에서 프로게이머를 상대로 AI가 이겼다는 블로그 소식을 접한바 있다. 이 게임은 내가 잘 모르는 게임이지만, 이 행사(2018년 8월 5일)가 가지는 의미는 multi-agent환경에서 매우 복잡한 전략 다른 agent들의 전략을 추론하며 게임을 한다는 것이다. AlphGo도 의미를 가지지만 이 것도 매우 큰 의미를 가지는 것이 틀림 없다. Dota-2대신에 StarCraft였으면 훨씬 재미있었을 것이다.

여하튼, 이 알고리즘이 어떻게 구현되고 실행되는지 살펴보기 위해 이미 공개된 코드를 사용하여 재현해 보았다. 큰 줄기만 살펴보는데도 코드 해석에 무척 애를 먹었다. 아래 동영상은 OpenAI의 multi-agent environment에서 simple_tag라는 scenarion를 MADDPG로 학습한 결과를 보여준다. 이 scenario는 녹색 agent가 적색 adversary agents들로부터 붙잡히지 않고 검은색 목표지점으로 이동하는것을 목표로 한다. 이 코드는 위에서 설명한 policy ensemble을 사용하지 않았다.

Simulation | ML

for personal research projects

Multi-Agent Actor-Critic RL

Multi-agent MDP와 DDPG

Multi_agent Actor-Critic

Agent policy 추론

Agent Policy Ensembles

테스트

게시자: jayyang

댓글 남기기 응답 취소

Multi-agent MDP와 DDPG

Multi_agent Actor-Critic

Agent policy 추론

Agent Policy Ensembles

테스트

이 글 공유하기:

관련

게시자: jayyang

댓글 남기기 응답 취소