Simulation | ML

Meta Learning분야에서 유명한 논문중에 Model-Agnostic Meta Learning이라는 논문이 있다. Agnostic이라는 단어가 특이해서 기억하고 있는데, 같은 단어를 사용하는 논문이 발표되었다. 매우 흥미로운 논문이라 소개하고자 한다. 이 글의 제목이 그 논문의 제목이다.

이 논문의 촛점은 Neural Network Architecure(구조)에 관한 내용이다. 우리는 이미지 분야의 신경망에 매우 다양한 신경망이 개발되었고 그 신경망마다 고유의 이름을 갖고 있다는 것을 알고 있다. 이미지 분야에서는 더 적은 수의 weights를 가지지만 더 정확한 정확도를 가지는 신경망 구조라고 주장하는 글들을 많이 볼 수 있다. 사실 인공지능의 연구는 이러한 인공 신경망의 구조에 대한 연구라고 할 수 있다. 우리가 학습시키는 과정은 인공 신경망이 가지는 weight라고 불리우는 tunning parameter들을 fitting하는 과정이다.

그러나 신경망구조는 연구자의 경험에 의해 선택되어 지는 구조이고 학습하는 알고리즘은 이미 정해진 신경망 구조가 가지는 weight를 목적에 맞게 조정하는 과정이다. 이와는 반대로 접근해보자는 것이 이 논문의 저자가 시도한 approach이다. 학습하려는 solution 자체를 품고 있는 신경망 구조를 만들어 내기 위해서는 weight 자체의 비중을 줄여야 한다. Weight를 distribution에서 sampling하는 Bayesian Neural Network와 같이 weight를 sampling하여 사용하되, 하나의 통일된 값을 사용한다. 이 처럼 특정값으로 학습시키지 않고 sampling하는 방법으로 network topology만의 성능 평가가 가능하다. 한마디로 말하면, weight는 모두 같은 값으로 하고, 신경망의 구조를 학습시켜 최적의 신경망구조를 찾아 보자는 것이다. 즉, weight를 학습하는 것이 아니라, 신경망 구조 자체를 학습하는 것이다. 그러므로 weight학습에 의한 효과를 최소화 시키고 신경망 구조에 대해서만 성능 평가가 가능하도록 하고 구조의 성능순위를 이용하여 계속해서 구조를 진화 시키도록 하였다. 아래가 그 개념을 설명하는 그림이다. 두 번째 step에서 weight를 sampling하여 평가하되 모든 weight는 동일한 값(sampling 된 값)을 사용한다.

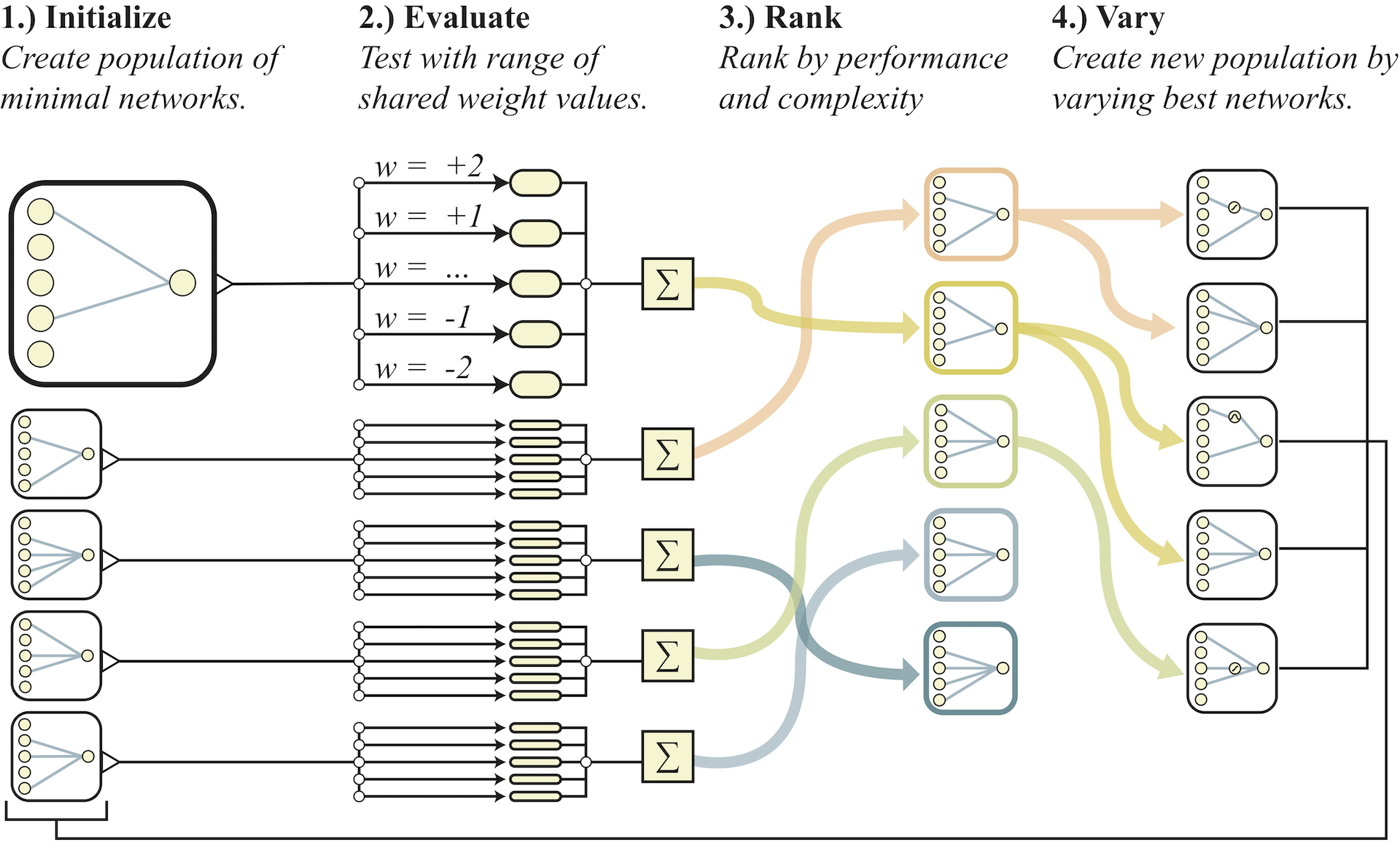
그렇다면 step 4에서 topology를 변화시키기 위해 어떤 방법을 사용한 것일까? 아래 그림이 그것을 잘 설명하고 있다.

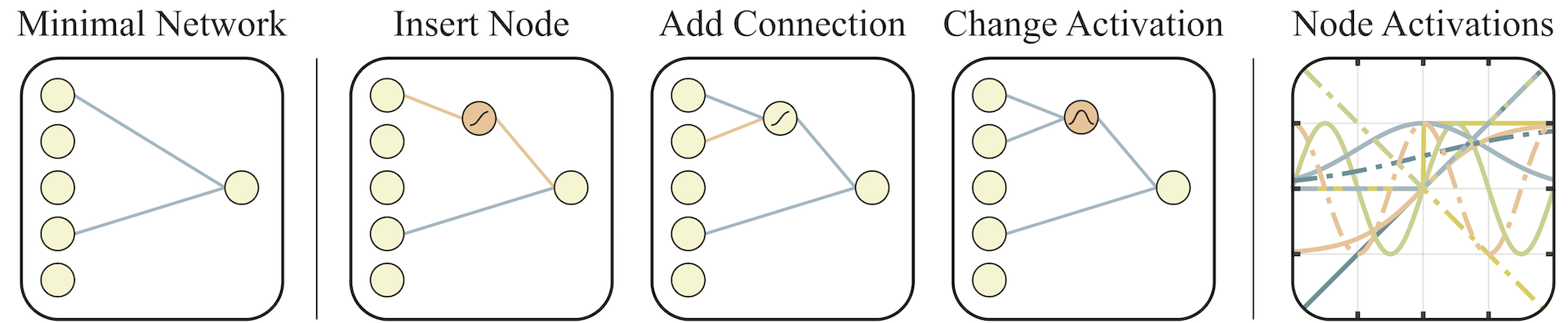
Step4에서 보여주는 구조들의 순위(rank)는 매기기 위해 어떤 평가 항목들을 사용했을까? 여러 weight 값을 사용한 구조의 평균 성능치, 최고 성능치, network의 연결수를 사용했다고 하며, network의 연결수라는 것은 같은 성능이라면 topology가 단순한 것을 우선하였다는 의미이다.

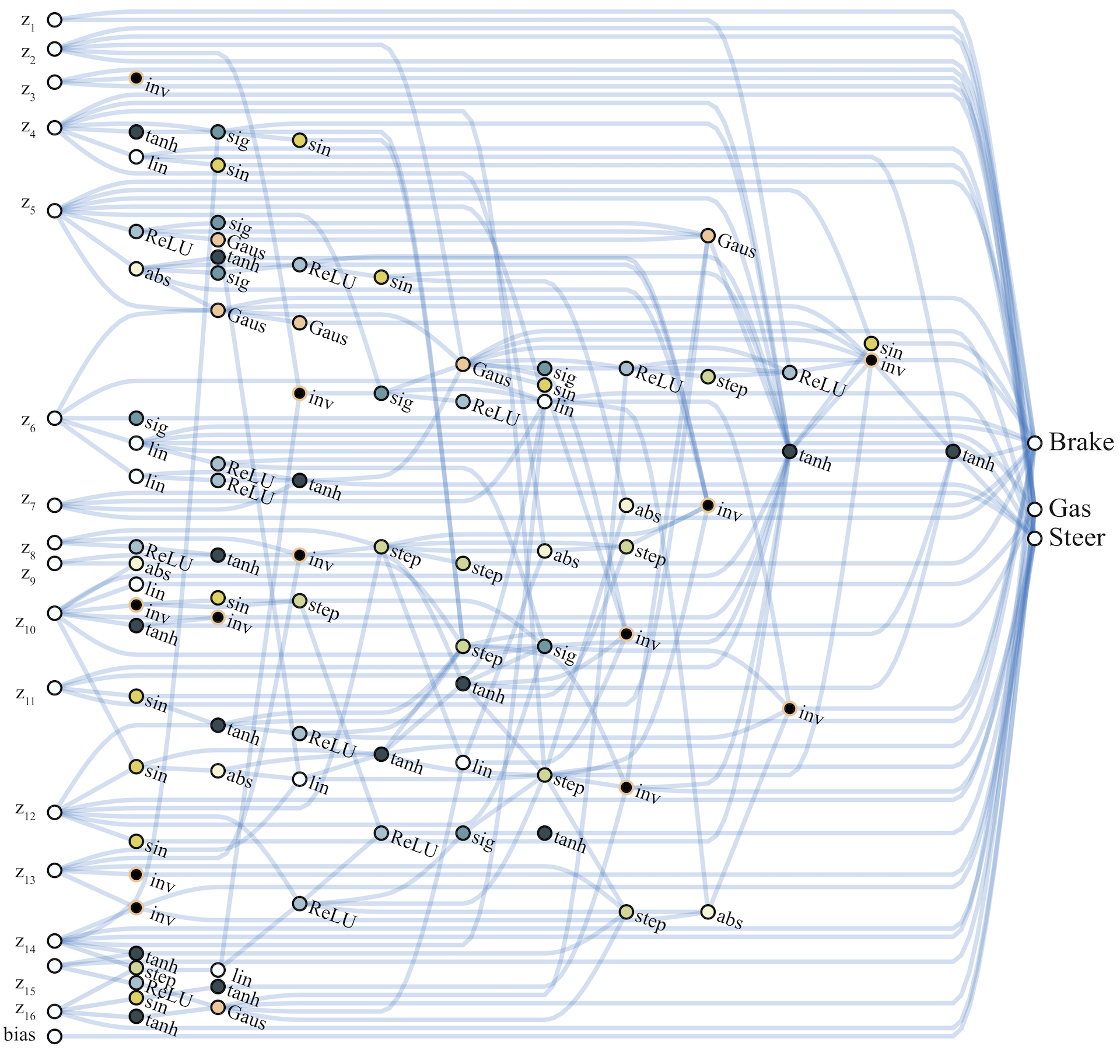
이렇게 찾아낸 topology는 어떤것일까 궁금하다. Swing-up task의 Topology를 찾은 과정에서 8세대와 32번째 세대의 network구조를 아래 보여주고 있다. Swing up task의 force를 알아 내기 위해 사용된 network가 세대를 감에 따라 보다 복잡하고 다양하게 엮이는 것을 볼 수 있다. 밑의 그림이 최종적으로 찾아낸 구조이다.

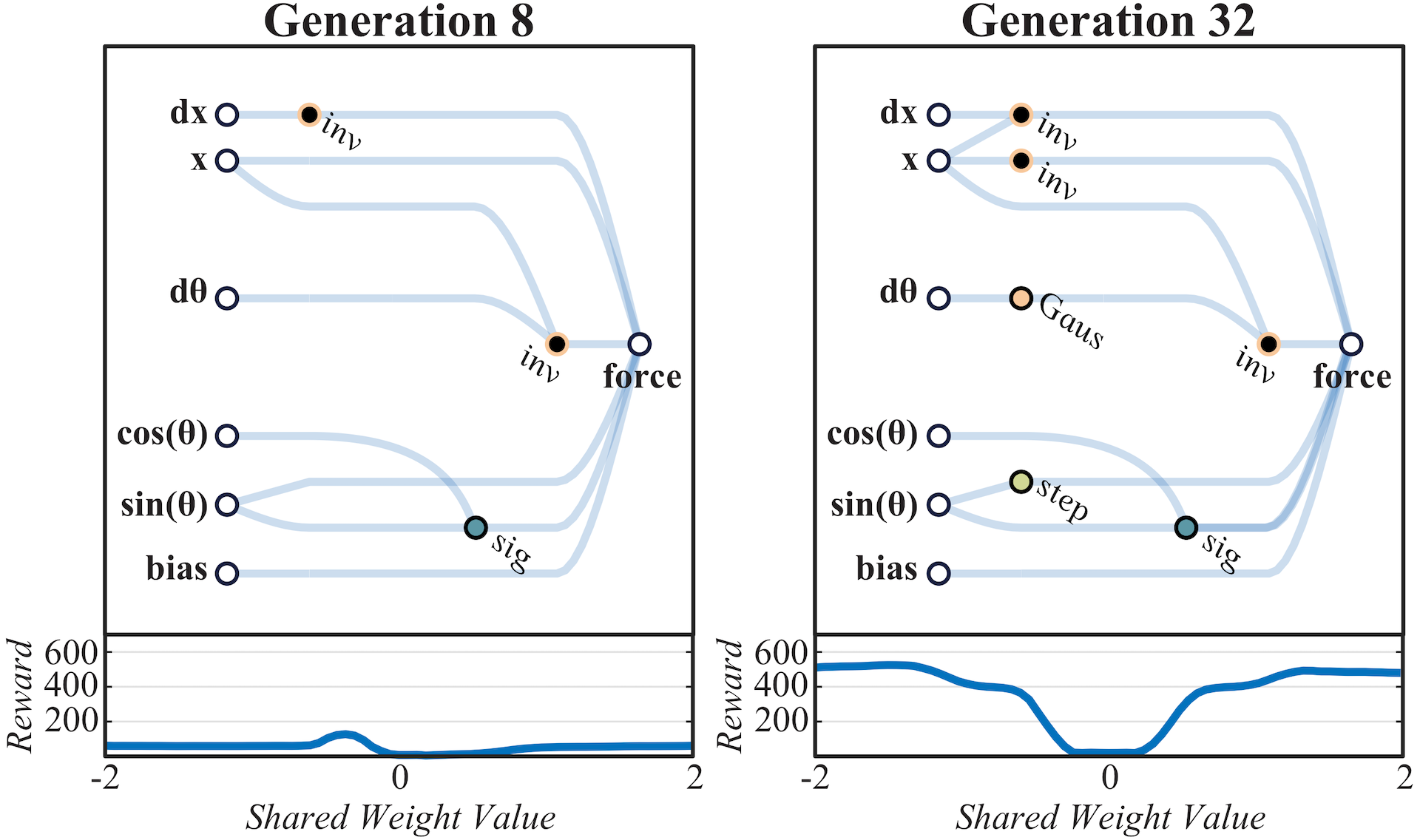
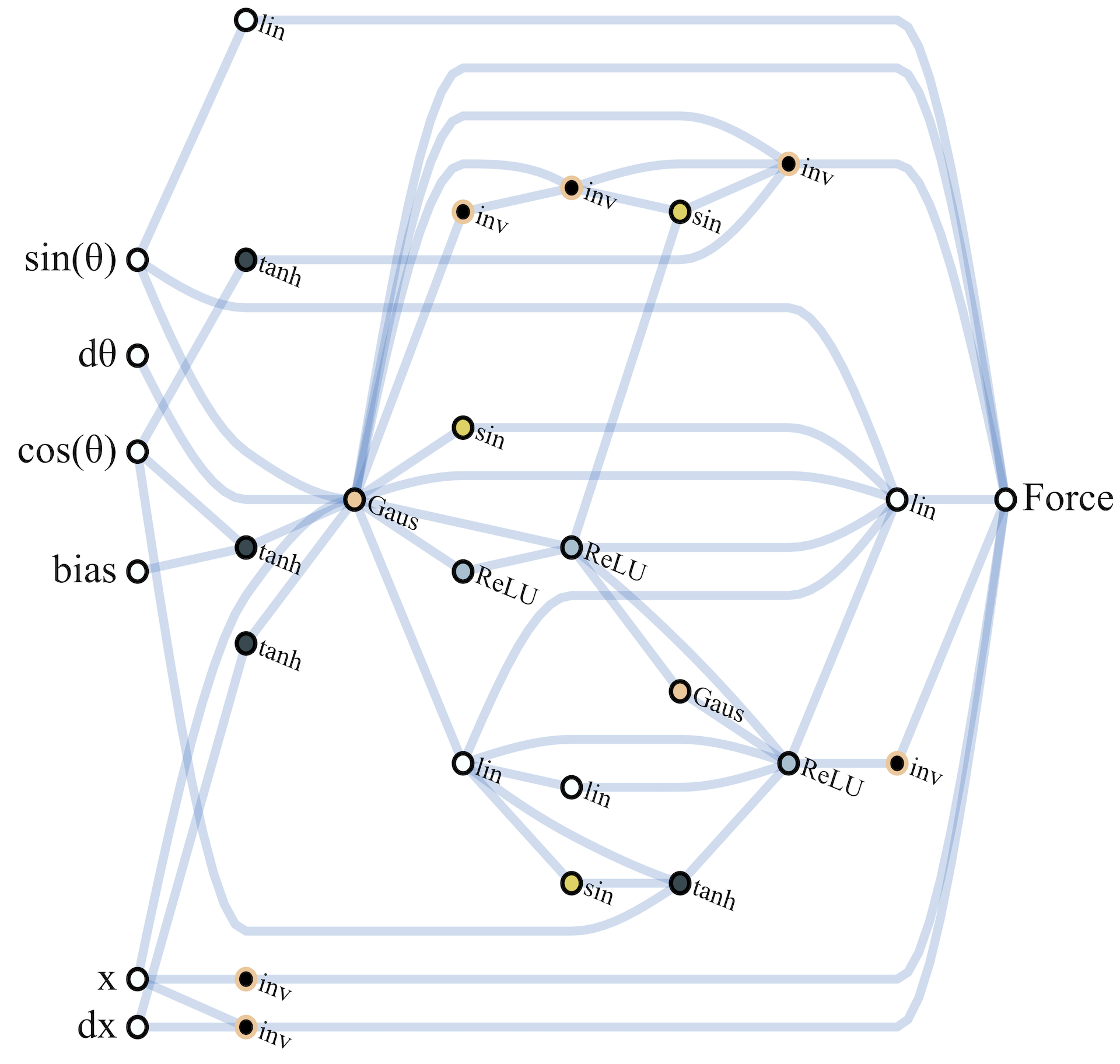
이러한 방식으로 찾아낸 topology가 어느 정도까지 복잡하게 진화 할 수 있는지를 보여주는 그림을 하나 더 소개하면 car racing은 아래 그림과 같은 구조를 찾아 냈다고 한다.

이제 이 이론의 성능을 살펴볼 차례이다. 아래는 논문에서 밝힌 3종류의 continuous control tasks의 성능 비교표이다. Continuous control task는 이 블로그의 RL section에서 많이 소개한 task이다.

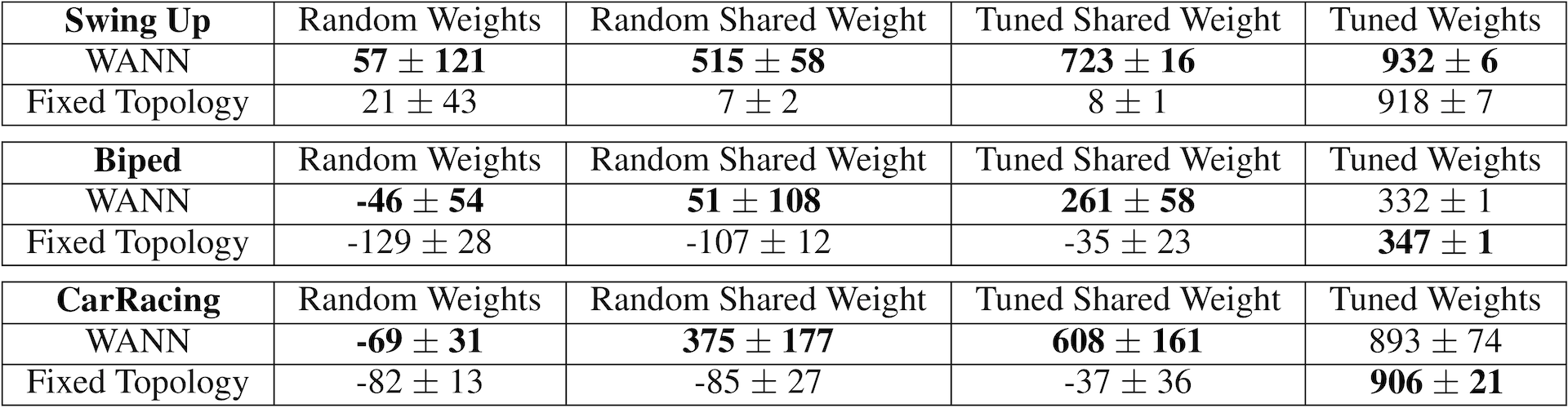
이 성능 비교표는 많은 정보가 포함되어 있으며, 이 결과는 이론을 접했을 때 내가 예상한 결과와 유사하다. 이 표에서 보여준 방법중 Random Shared Weight가 순수한 이 이론의 결과이다. Tuned Shared Weight는 공유하는 하나의 weight를 학습시켜 얻은 값을 사용한 성능이다. Tuned Weight는 weight를 공유하지 않고 최적이라 생각하는 구조의 weight를 기존의 방법과 같이 학습시켜 얻은 결과이다. WANN방법이 기존의 방법과 그다지 큰 차이를 보이지 않는다.

이 결과는 어찌보면 당연한 결과로 생각든다. 우리가 특정 변수를 regression한다고 할때, 함수를 선정(여기서는 Fixed network와 비유된다)하고 인자를 변화시켜 최소의 error를 가지는 함수의 parameter(여기서는 weight)를 찾아 낸다. 이것이 기존의 fitting 방법이지만, 이 논문이 사용한 방법과 유사하게 parameter는 모두 하나의 값(예를 들어 1.0)으로 고정하고, 다양한 함수를 조합(선형, 비선형 함수의 다양한 수학적 표현)하는 시도를 해보면 변수의 예측 error를 최소화 하는 함수를 찾을 수 있다. 그러나, 이것도 일종의 함수를 변화시키는 fitting이며 수학적으로 접근 방법이 다를뿐 그 결과면에서 큰 의미를 가진다고 할 수 없다. 예를 들어 parameter를 0.5로 고정하고 찾는 함수는 1.0으로 고정하고 찾은 함수와는 다른 구조가 최적일 것이다. 이러면 찾아낸 topology에 대한 의미가 퇴색된다. 이러한 허점을 보완하고자 다양한 weight를 sampling한 종합 평가 결과를 구조의 순위를 매기는데 사용한 것이다.

최종적으로 얻은 최적의 topology라고 할지라도 결국 그 한계는 분명하다. weight 중심의 adaptation이든 함수 중심의 adaptation이든 결국은 상호 연관되어 있다. 이 논문에서 시도한 바와 같이 WANN을 이용해 찾은 최적의 network구조라고 할지라도 weight까지 학습시켜 얻은 결과는 기존의 방법과 결과가 다르지 않다. 다만, 학습의 과정이 몸체(topology) 학습단계(1단계)와 weight학습단계로 구분한다고 하더라도 결국은 크게 다르지 않음을 보여준것이다. 몸체 학습단계가 Fixed network와 형식적으로는 많이 달라 보여도 수학적 기능관점에서 크게 다르지 않기 때문이다. 기존의 과학과 같이 자연을 설명하는 수학적 표현은 그것이 다양한 가정에 의존한 것일 지라도 논리적 근거를 가지고 도출되고 실험에 의해 수학적 표현에 포함된 parameter를 fitting하는 방법이 더 합리적 접근법이라고 생각된다. WANN이 흥미로운 접근 방법이기는 하지만 뇌과학과 같은 연구에 의해 되도록 뇌의 기저를 이해하고 이에 기반한 topology를 사용하는 것이 보다 나은 방법론으로 생각한다.